Here is Jon's derivation for the formula. Now I don't feel so bad that I couldn't figure it out for myself!

Derivation of formula for distance from lower bout of guitar to position of highest point of arched back.

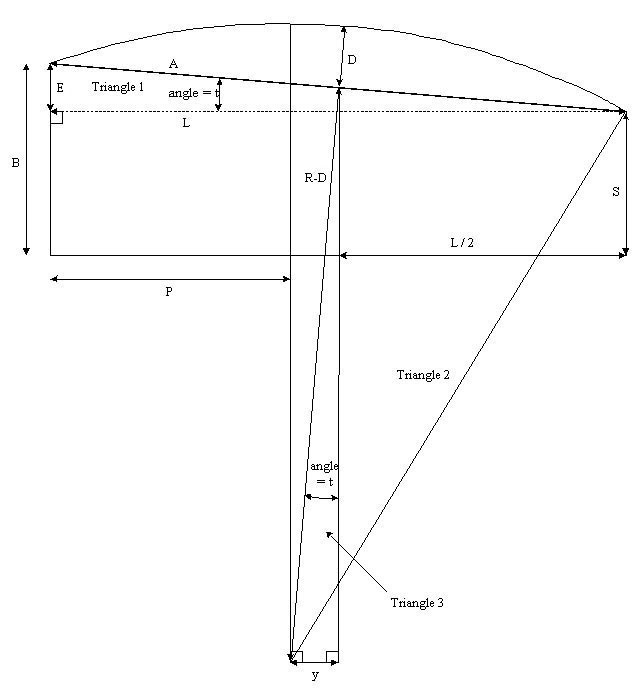
Quantities:
S = height of guitar sides at neck block
B = height of guitar sides at end block
E = B - S (difference in height at shoulders and butt)
L = length of guitar body
A = length of body measured at angle (see diagram)
D = deflection in arched back (see diagram)
R = radius of back arch


Key observation: Triangles 1 and 3 are similar, so their angles t are equal.


Triangle 1: Pythagoras
A^2 = L^2 + E^2


Triangle 2: Pythagoras
(R - D)^2 + (A/2)^2 = R^2
or
R - D = sqrt( R^2 - A^2/4 )
= sqrt( R^2 - (L^2 + E^2)/4 ) (using Triangle 1 Pythagoras)
= sqrt( R^2 ( 1 - (L^2 + E^2)/4R^2 ) )
= R sqrt( 1 - (L^2 + E^2)/4R^2 )


Triangle 1: Trigonometry
sin(t) = E / A
= E / sqrt( L^2 + E^2 ) (using Triangle 1 Pythagoras)


Triangle 3: Trigonometry
sin(t) = y / (R - D)
or
y = (R - D) sin(t)
= R sqrt( 1 - (L^2 + E^2)/4R^2 ) sin(t) (using Triangle 2 Pythagoras)
= R sqrt( 1 - (L^2 + E^2)/4R^2 ) E / sqrt( L^2 + E^2 ) (using Triangle 1 Trig)
= R E sqrt( (4R^2 - (L^2 + E^2)) / (4R^2 ( L^2 + E^2 ) ) )
= E/2 sqrt( (4R^2) / ( L^2 + E^2 ) - 1 )


Finally:

P = L/2 - (E/2) sqrt( (4R^2) / ( L^2 + E^2 ) - 1 )