Intonation II

| Previous article | Next article |

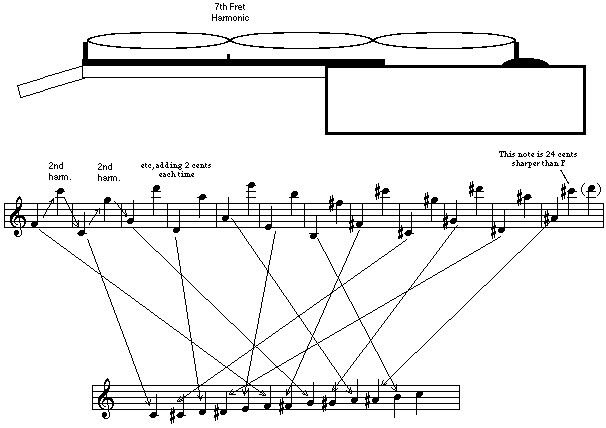
In Intonation I, I presented the first of a short series of articles on intonation. Getting guitars to play in tune on every fret up the neck is one of the most common repair tasks, and one of the most critical parts of building new instruments as well. I hope you enjoy the articles. Meanwhile, please visit my website www.DoolinGuitars.com for a look at some guitars which not only play in tune all the way to the 22nd fret, but let you get there without making pretzels of your left hand fingers... In Intonation I I showed how the Harmonic Series implies the 12 tones of our chromatic scale, as well as the seven of those tones which we most commonly use as our diatonic major scale. I also pointed out that the distance between these tones is not consistent, leading to discrepancies in intonation. The early history of (Western European) music describes the discovery of these discrepancies and various attempts to cope with them. In fact, with each breakthrough advance in harmony usage, new adjustments, or temperaments, were devised to accommodate the increasing sophistication in harmony. In this article, I'll describe the main temperaments and their corresponding musical periods. To compare distances between notes I'll use cents (pronounced "sonts"), a quantity of pitch change equal to 1/100 of a half-step, or 1/1200 of an octave. This system is very convenient for illustrating the strengths and weaknesses of each temperament, and avoids a lot of hairy math associated with the logarithmic response of the ear to pitch. So here they are, four approaches to producing a set of tones which work together in tune: Pythagorean Temperament Named after the Greek mathematician Pythagorus, who discovered the Harmonic Series while experimenting with early string instruments. The scale is built by striking the second harmonic of the string (the harmonic on the 7th fret of the guitar), producing the fifth scale degree, then tuning the string to the new note and striking the second harmonic of that note, etc. around the cycle of fifths. Do this 12 times and you end up where you started... almost. Unfortunately, you actually end up twenty-four cents sharp, or two cents per iteration. This is what you're doing when you tune the lower four strings of the guitar by matching the harmonics on the 5th and 7th frets of adjacent strings. It comes pretty close to getting the guitar in tune, since you've only gone 6 cents sharp by the time you tune the D string (again, two cents per iteration). Compared to the Harmonic Series, this scale has very sharp 3rd degrees (22 cents sharper than the Harmonic Series) but the fifth interval is perfectly Just (in tune with the Harmonic Series). This temperament worked great for the parallel fifths in Gregorian chants, but when harmony in thirds became popular those sharp thirds became annoying. To pull the thirds down into agreement, Meantone Temperament was developed. Meantone Temperament If you shave a little off of each fifth interval as you generate your scale, you can adjust the intervals in various ways. One popular system shaved five cents from each new interval, resulting in a third scale degree which agrees perfectly with the Harmonic Series. This works beautifully with Renaissance music featuring contrapuntal lines which form thirds. However, if you follow this method all the way around the circle of fifths, you end up 36 cents flat. 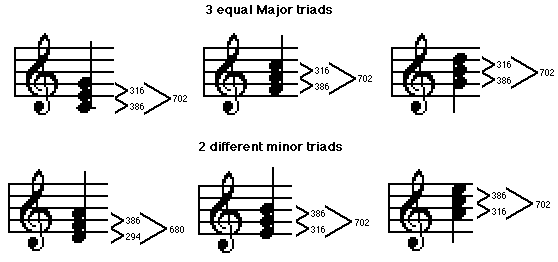Moreover, as soon as someone stacked another third on top to create triads, those slightly flat fifths didn't sound so great. So why not generate a scale from the beautifully consonant triad from the Harmonic Series? Just Temperament By adjusting the scale tones such that the three major triads in the scale (the I, IV and V chords) all agreed with the Harmonic Series based on their respective roots, a scale results which is perfectly consonant for early triad-based classical music (and modern country-western I suppose). Unfortunately, Just Temperament produces 2 different sizes of whole steps, and consequently 2 sets of intervals for minor triads. Further discrepancies occur in the chromatic half-steps, making any key more than a couple of sharps or flats away badly out of tune. I, IV and V established true tonality, and along with it, the possibility of contrasting different tonalities - modulation, minor vs. Major keys, borrowing chords from minor within a major tonality, temporary modulations, substitute dominant harmonies, and all the other wonderful devices which twelve-tone harmony offers. Just Temperament offers perfect agreement with the Harmonic Series only in the tones of the I, IV and IV triads and only in the Major key of the I chord. 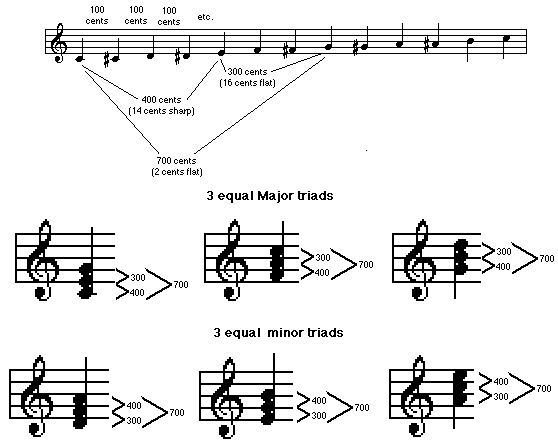In fact, none of the above temperaments offers consistent intonation for all keys. The only way to make intonation consistent is to make all of the half step intervals consistent - all the same size. This leads us to... Equal Temperament Actually a form of Meantone Temperament, this system shaves just two cents from each fifth around the cycle, which gets you back to exactly the same pitch you started with. As a result, all twelve half steps are exactly the same size so any triad from any scale step also has intervals of the same size. This means that any key, modulation or tonality works as well as any other. I say "as well as any other" because Equal Temperament has similar problems to those of Pythagorean Temperament - sharp thirds. They're not as sharp - only fourteen cents rather than twenty-two cents - but sharp enough to sound a bit bright and dissonant compared to "Just" thirds. In Intonation III, I'll make a lot of folks mad by stating the case for Equal Temperament as the only practical tuning system for modern guitars. Meanwhile, I'll look for your suggestions and questions in my mailbox... E-Mail Me For an in-depth discussion of temperaments and other topics in acoustics, read "The Acoustic Foundations of Music" by John Backus (W. W. Norton & Co). This book is the source of much of the information for this article series.

| Previous article | Next article |