Calculating Side Contours
|
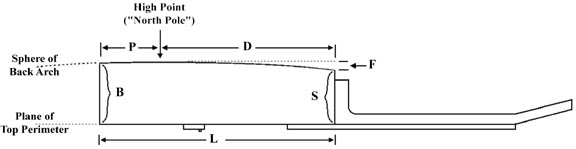
Note: Michael Darnton's article "Tales of Topographic Arches" in American Lutherie#78 p.45 describes a much simpler graphical method of calculating side depths. I have switched to his method myself, and only include my article here in hopes that it might be of interest to luthiers who enjoy a mathematical approach. Back in AL #58 Jon Sevy published the article 'Calculating Arc Parameters', which described how to calculate the radius, length or depth of a curve. I've used these formulas extensively ever since, for radiusing fretboards, making dished workboards, calculating neck angles, and even non-lutherie shop tasks. Recently it occured to me that one could use these formulas to calculate the height of a guitar's side at any point. If the guitar has a spherically domed back, the back falls off from its highest point in an arc in every direction:
This "high point" is effectively the North Pole of the sphere from which the back arch is taken. If we assume a top whose perimeter is all in the same plane, that plane intersects a line of latitude on that sphere. The high point is therefore the point on the back which is farthest from the plane of the top perimeter. All measurements of side height are then distances between that plane and the surface of the sphere of the back arch. I adapted Jon's formula to calculate the falloff from the high point on the back to any point on the side.
F = R - SQRT(R^2 - D^2) where
Adapting this formula to account for the thickness of the top and back and to yeild direct measurements of side height: H = ((B+(R-SQRT(R^2-P^2)))-(R-SQRT(R^2-D^2)))-(M+N)
If the body is deeper at the butt than it is at the shoulders, the high point is going to be closer to the butt than to the shoulders, typically about 3 inches in. The closer the high point is to the butt, the more the side height will taper toward the neck. I reasoned that if you knew the height of the side at the shoulder and at the butt, and knew the radius of the back, those three factors would determine where the high point would fall. However, I realized after a couple of days of head-scratching that I don't have the math chops to derive the formula. A quick online search and an e-mail put me in touch with Jon Sevy himself, who responded in just a few hours with the following formula: P = (L/2) - (E/2)sqrt((4*R^2)/(L^2 + E^2) - 1)
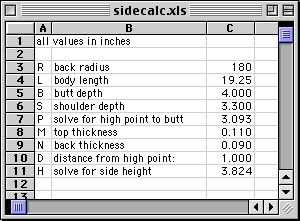
See the sidebar for the derivation for this formula. Armed with these two formulas, I created an Excel spreadsheet to do the calculations. Here are the Excel formulas: solve for high point to butt
solve for side height
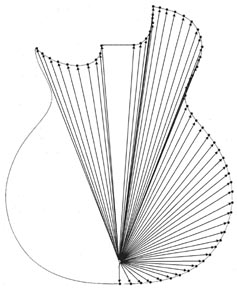
I first enter the "back radius", "body length", "shoulder height" and "butt height" for my guitar design. This will calculate P, the distance from the high point to the butt, in "solve for high point to butt". Then I can calculate the height of the side at any point. To do this on a new guitar design, I trace the outline of the body onto a big piece of paper, mark it off in one-inch increments all around the side, mark the calculated high point, and measure the distance from the high point to each mark:
Then I plug each measurement into "distance from high point", and the answer "solve for side height" is the height of the side at that point. I transfer these measurements to the back edge of the side at each inch increment, connect the dots, and trim to the line. "top thickness" and "back thickness" are subtracted from the measurements to give the actual side measurement. The great thing about this method is that it calculates cutaway side pieces just as easily as the main sides. I made plexiglas side templates for all my standard body body shapes, so now I just trace from the templates directly to the sides. But when I get a custom order or decide to add a new body style to my product line, I can make side templates for the new shape and know that the sides will be correctly contoured. It's important to note that you must register the sides carefully when bending them. If the various measured heights don't fall where they should on the body outline, the contour will not match the spherical section. Also, you'll need to allow for the thickness of the sides when taking the distance measurements on the tracing of the body outline. Make sure that the tracing is not larger than the actual shape of the finished body, e.g. by the thickness of the pencil lead or because of poor fit of the bent sides in the mold. Any discrepancy between the tracing of the body shape on paper and the actual outline of your bent sides can throw the contour off. If you use a very flat back arch with a large difference in the butt and shoulder heights, you will get a negative number for "solve for high point to butt". This means that the high point is actually behind the butt, off the body of the guitar, and that the angle between the back and the sides at the butt will be less than 90 degrees. Just trace your body outline on a piece of paper large enough to mark the high point behind the butt, and take your measurements from there. These formulas can be used to calculate side contours for wedge-body guitars as well (ergonomically designed guitars which are deeper on the treble side than on the bass side of the body). First, decide on the height of the side at the widest part of the lower bout on both the bass and treble edges, to create the wedge. Plug the bass edge measurement into "shoulder height" and the treble height into "butt height", and use the width of the body for "body length". The answer in "solve for high point to butt" is the distance from the treble edge to the high point, which will be offset to the treble side of center. Mark this point and draw a line through it parallel to the center line of the body. Then calculate the high point as usual, but mark it on the offset line. Now you can take all your measurements from this offset high point to calculate the side contours for your wedge body. E-Mail Me
|