Intonation IV

| Previous article | Next article |

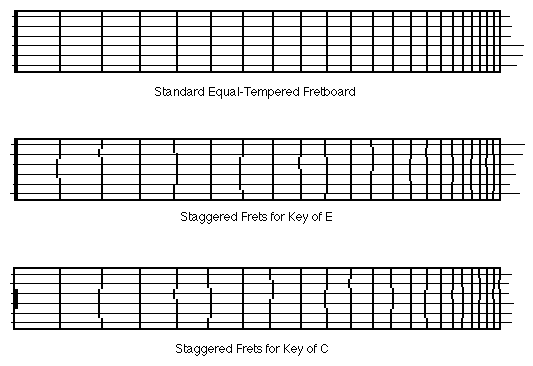
In Intonation I I showed how the Harmonic Series implies the 12 tones of our chromatic scale, as well as the discrepancies in the distance between these tones which lead to discrepancies in intonation. Intonation II described the main temperaments and their corresponding musical periods. In Intonation III, I hope I made the case for equal temperament as the best compromise for modern music. In this article I'd like to show how all of this applies to the guitar. The Equal Tempered Fretboard As I mentioned in Intonation III, the spacing of the frets on the guitar fretboard is Equal Tempered. Mathematically this means that each successive fret is closer to the bridge by a factor of the 12th root of 2; that is, the number which when multiplied by itself 12 times equals 2. This isn't really all that weird - if there are 12 frets to the octave, and the pitch at the octave is twice that of the open string, the 12th root of two simply divides the octave into 12 logarithmically equal parts, satisfying the ear's logarithmic response to frequency. This explains why the frets get closer together the higher you go, while the pitch difference between each pair of frets is always one half-step. But more importantly for fretted string instruments, Equal Temperament generates the same fret spacing for any string tuned to any pitch. This allows for straight fret slots which are parallel to the nut - something we're all accustomed to seeing. Any other temperament system would create some pretty strange-looking frets, since the spacing would vary depending on what interval of the scale occurred at a given fret and string. The frets would be "broken" or "staggered" across the fretboard, and a different placement would be required for each key! Such fretboards have been made in the past; one system I've seen used replaceable fretboards to allow the player to switch temperaments for different musical pieces. 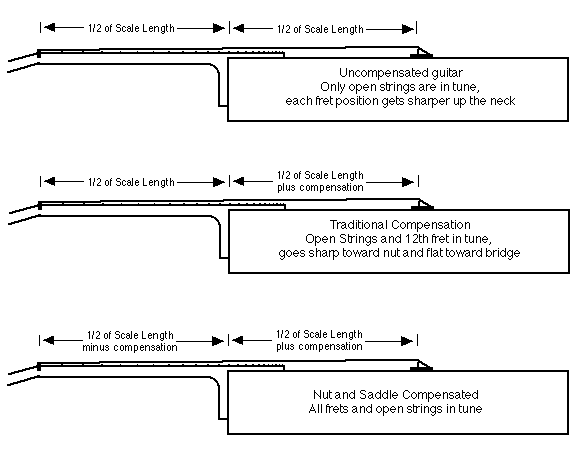While there may be a place for this sort of thing, the vast majority of guitarists simply want their regular old fretboards to play in tune. The good news is that this isn't asking too much since the frets of most guitars are placed accurately according to Equal Temperament. The bad news is that most guitars fail to achieve Equal Temperament due to incorrect saddle and nut placement. Let me emphasize this point: before we blame Equal Temperament for the intonation woes of guitars, let's be sure we've actually achieved Equal Temperament in the first place! To do so, we must do two things: get the saddle and nut placement right, and tune the strings correctly. Saddle and nut placement is the luthier's responsibility, whether the luthier in question is the original builder of the guitar, a qualified repair person, or the owner of the guitar who does his or her own repairs. Tuning the strings is the player's responsibility, or in some professional situations, the guitar tech's. As I will describe below, there is more to these techniques than common knowledge would suggest. In other words, there's more to guitar intonation than adjusting the saddle, and there's more to tuning a guitar than 7th fret harmonics and sweet-sounding open-E chords. Intonation 101 First, a quick review of standard intonation technique. The guitar's bridge is placed on the top such that the 12th fret is at the midpoint of the strings. This makes the pitch at the 12th fret one octave above that of the open string, or twice the frequency. The nut is placed at the "zero fret" position, and fret positions are calculated from it using the 12th root of 2 formula. Fretting the string shortens its length by some multiple of the 12th root of 2, according to which fret is used, yielding a pitch which is an Equal Tempered interval above the open string's pitch. The theoretical position of the saddle in the bridge is exactly twice as far from the nut as the 12th fret. I say "theoretical" because the act of fretting the string bends its pitch sharp, to a degree determined by the gauge and material of the string, action height, scale length and open-string pitch. To compensate for this sharpening, the saddle is moved away from the nut, which lengthens the string to make it sound flatter. Since so many factors affect how sharp the string goes when fretted, there is no standard amount of compensation which works for every guitar. To play in tune, every guitar needs its saddle position fine-tuned for the strings and tuning to be used. On most electric guitars, this is accomplished with individual screw-adjustable saddles, while on most acoustic guitars the bone saddle must be shaped to set the point of string termination within the saddle's width. Either way, the length of each string is adjusted to compensate for the sharpening of its pitch when fretted. Intonate the Nut? OK, that's how we've all been taught to intonate guitars. But does it really do the job? Consider the nut, or open-string pitches. We compensate for the sharpening of pitch due to stretching the strings down to the frets by adding saddle compensation. Well, it's the same story at the nut: the higher the nut action, the more compensation is needed. What do I mean by nut action? If you imagine the plane of the frets (assuming for a moment that there is no "relief", a perfectly flat fretboard) running from the last fret to the first, and then extending to the nut, the bottom of each nut slot relative to that plane determines nut action. If the nut slot is cut so it exactly meets the plane of the frets, there is effectively zero nut action. If the slot is cut deeper than that, the open string will certainly buzz on the first fret - time for a new nut. But if the slot is cut more shallowly, so it comes short of the plane of the frets, that distance is what I refer to as nut action. And the shallower the slot, the higher the nut action, the sharper the string goes, and the more nut compensation is needed. But what does this mean when we tune the guitar by tuning the open strings and intonate the saddle from there? It means that the open strings and the 12th fret are the only pitches which are really in tune! If you test the pitches at each fret of a traditionally intonated guitar, you'll find that the pitches go progressively sharp as you move backwards from the 12th fret to the nut, and progressively flat as you move up from the 12th fret towards the bridge. This effect is more subtle than that of an uncompensated saddle, but is significant and quite audible. The solution is nut compensation. Like saddle compensation, the nut is moved away from its theoretical position to change the string length, to varying degrees according to string type and pitch. Since the sharpening effect of high nut action makes the open strings flat relative to the fretted notes, moving the nut closer to the saddle will compensate by shortening the string, so the open string pitches go sharp to the same degree. In other words, the end of the fretboard is shaved slightly short, moving the nut toward the bridge. Nut compensation has been researched extensively by two classical luthiers, Greg Byers and John Gilbert. They have taken different approaches to the problem, but both have achieved good results. John Gilbert's solution is to shave about one thirty-secondth of an inch from the end of the fretboard, applying the same amount of compensation to all the strings (just as the straight saddle on the classical guitar does at the bridge end). For new designs he accomplishes this by using a longer scale fretboard than the actual scale length, without changing the nut or twelfth fret location. For example, he uses a twenty-six and one-thirty-second inch scale fretboard on a twenty-six inch scale guitar and shaves a bit from the nut end of the fretboard. John has used this system since 1978 with excellent results, as confirmed by his many satisfied clients. Greg Byers did extensive mathematical modeling of string compensation, which yeilded specific compensations for each string at the nut and saddle. To confirm the results of his theoretical model, he attached a fixed fretboard and movable "nut" and "bridge" sections to a long plank and moved the nut and bridge to find correct nut and saddle compensation. Each string is mounted on the device and the ends are adjusted until each fret and the open string read in tune; the distances to the nut and saddle are then measured and transferred to the instrument. This yields both staggered nut and saddle. Byer's method results in individual compensation per string, an improvement over Gilbert's equal compensation. Both luthiers note, however, that the amount of compensation is slight and that they are both working toward the same end. Or set the Nut Action? On my own instruments, I find that if i get the nut action as low as possible for a given instrument and player, I usually don't need nut compensation. But some setups do require it. The point is to realize what is causing the need for nut compensation (the sharping effect of nut action), and to treat each each instrument individually, compensating only as needed. As a starting point, I set my nut action to about .010" on the top four strings and .020" for the bottom two on steel string guitars, and about double that for nylon string guitars. I do this by measuring the height of the first fret, stacking up feeler gauges to that height plus the nut action desired, slide the feeler gauge stack under the strings up against the nut, and file the slot until the file just touches the feeler gauge. From there, I look at and feel the action at the first fret; if I think I can lower the nut action on any string I do so a few thousandths at a time. Then when the nut action is as low as I feel I can get it, I check the first fret intonation relative to the open strings, and if I'm still seeing any strings going sharp at the first fret, only then will I shave the end of the fretboard. In the next article... I'm running out of space, so I'll have to talk about pianos and guitars in Intonation V. I'll also talk about the new "Tuning Systems" being offered as alternatives to traditional intonation, and conclude this series of articles by suggesting a technique for correctly tuning a guitar once it is correctly intonated. Meanwhile, I'll look for your suggestions and questions in my mailbox... E-Mail Me For an in-depth discussion of temperaments and other topics in acoustics, read "The Acoustic Foundations of Music" by John Backus (W. W. Norton & Co). This book is the source of much of the information for this article series. For an in-depth discussion of nut and saddle compensation, read Greg Byers' article "Classical Guitar Intonation" in the Fall 1996 issue of American Lutherie.

| Previous article | Next article |