Intonation V

| Previous article | Next article |

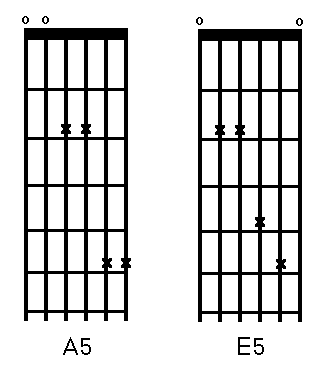
In this article I'll describe a technique for correctly tuning a guitar once it's correctly intonated, along with some thoughts about alternatives to traditional intonation, and intonation problems between pianos and guitars. I hope you've enjoyed the articles. Also, please visit my website www.DoolinGuitars.com for a look at some guitars which not only play in tune all the way to the 22nd fret, but let you get there without having to learn Yo-Yo Ma's left hand thumb technique... But I still can't get my guitar in tune... Assuming your guitar is completely intonated (frets correctly placed, nut and saddle compensated, good new strings), the instrument is still a challenge to tune. This is because any string may carry any of the 12 possible tones during a given piece, and errors tend to compound. Unfortunately, many players exacerbate the problem by trying to tune to 1st position triads, such as the ever-popular open E chord. In doing so, they'll tend to tune the A and B strings a touch sharp and the G quite a bit flat, in an attempt to make that E chord sound really good. They're actually tuning to the harmonic series of the low E, resulting in fifths tuned 2 cents too high and thirds tuned 14 cents flat. Obviously, "tuning to harmonics" has the same problem, since guitar harmonics are isolated pitches from the overtone series of the strings (as discussed in Intonation I. You can compensate a bit by intentionally tuning the third sharp and the fifth flat, but this is hard to do accurately. I've stumbled upon a simple and quick tuning system which avoids thirds entirely: Get the guitar "in the ball park" by tuning to a pitch reference, the 4th and 5th frets, harmonics, or whatever. Check your tuning by playing these two chords, adjusting until they sound equally in tune: The two chords shown will average out any discrepancies because they only contain roots and fifths, and because the root of one is the fifth of the other and vice versa. Since these chords contain only fifth and fourth intervals, and since an Equal Temperament fifth is two cents sharp and an Equal Temperament fourth is two cents flat, tuning this way splits any difference; the thirds are automatically in tune (to the Equal Tempered scale) due to fret placement. This should give you a guitar which conforms to Equal Temperament within the limitations of real-world strings and fret placement, which is pretty darn close. This means that any combination of notes anywhere on the neck should yield Equal Tempered intervals and chords, and will agree with any other instrument tuned to Equal Temperament. Unfortunately, we cannot include in this group of instruments the other great polyphonic instrument of Western music, the Piano. What About Stretch Tuning? While the basis of piano tuning is Equal Temperament, the behavior of real-world strings doesn't conform to that tidy theory. Way back in Intonation I, I showed how a string vibrates in whole-number divisions of its length, generating a fundamental frequency and a set of overtones whose frequencies are whole-number multiples of that fundamental. In reality, these pitches can vary considerably from that ideal due to the phenomenon of inharmonicity. The overtones of real-world strings are always a bit sharp due to the stiffness of the string - each smaller subdivision of the string's length requires a sharper deviation from the straight line, bending the pitch sharp. Inharmonicity is a pronounced and crucial element of piano tone in particular, but is present and important in guitar tone also. The reason for this difference in the degree of inharmonicity between the instruments is due to the great difference in length, diameter and tension of their strings. Any given piano string may be carrying as much or more tension as all six strings on a guitar! The smaller, lower tension strings of the guitar produce a truer overtone series, and the guitar's relatively louder fundamental tones tend to mask discrepancies. The greater inharmonicity in pianos creates a strange problem with their tuning. If a piano is simply tuned to Equal Temperament across its range, the clash between the markedly sharp overtones of the low strings and the fundamentals of the high strings make the instrument sound out of tune with itself! The solution: "stretch tuning", wherein the high and low registers of the piano are tuned higher and lower, respectively, to bring the low strings' harmonics into tune with the upper strings' fundamentals. Thus, the piano is intentionally tuned out of Equal Temperament, in order to sound in tune with itself. (Note that this has nothing to do with temperament, which refers to the spacing of tones within the octave, regardless of register.) Happily for guitarists and pianists playing together, the stretch is not applied linearly; most of it occurs in the 1-1/2 octaves above and below the guitar's range. At the open low E and the 19th fret of the high E, the stretch is only about 5 cents, while anywhere on the top three strings up to the 12th fret is within 2 cents. The open high E is exactly in tune with the piano. While we're only talking about 2-1/2 cents per octave, the discrepancy is there, and shows why pianos and guitars can't ever be perfectly in tune with one another. Alternative Intonation Systems This problem of pianos and guitars has given rise to alternative intonation systems which attempt to bring the two instruments into agreement. These systems usually employ some variant of nut and saddle compensation, and/or stretched positioning of the higher frets, to simulate the stretch tuning of pianos. While it may be that a guitar set up in this manner could play in better tune with a piano, it cannot be in tune with itself, at least within the realm of Equal Temperament. Achieving Equal Temperament across the whole neck is the best all-purpose intonation solution. But Those Thirds Sound So Sharp... OK, I'll admit that even I have a hard time listening to those Equal Tempered thirds sometimes. And sometimes, I'll cheat, just a little, to get the effect of Just Temperament out of an Equal Tempered guitar. The way do this is to reserve a string for the third of the chord, tune that string down a bit, and play around it the rest of the time. The simplest example is to tune the open E chord to Just intervals, and play barre chord versions of that chord up and down the neck. As long as you only play that Major chord shape, it will be in Just Temperament everywhere on the neck. This may sound pretty limiting, and it is, but it's a trick that's been successfully used on thousands of studio recordings. This idea can be expanded upon by refingering more complex pieces of music so that the third always falls on the same string, moving anywhere on the neck to make that happen. Much beyond this though, and you'll start thinking about split frets, more than 12 frets per octave, B-Benders, pedal-steel style string stretchin' contraptions, hexaphonic pickups with hexaphonic harmonizers and MIDI presets to track your momentary temperament desires, DSP plug-ins and all-night digital editing sessions in the studio... beyond here lies madness. In the next article... When I originally wrote this series, Ithought this was the last Intonation article I'd write. But then I got a call from a reader that showed me that I had not done a very good job of explaining things. Intonation VI is my attempt to make ammends to the readers who were left scratching their heads. E-Mail Me For an in-depth discussion of temperaments and other topics in acoustics, read "The Acoustic Foundations of Music" by John Backus (W. W. Norton & Co). This book is the source of much of the information for this article series. For an in-depth discussion of nut and saddle compensation, read Greg Byers' article "Classical Guitar Intonation" in issue #47 of American Lutherie.

| Previous article | Next article |